Un po’ di matematica: Trasformazioni CSS in Internet Explorer 10

La proprietà transform, che abbiamo già osservato in un precedente articolo, ci offre delle comode funzioni per traslare, ruotare, scalare e piegare un blocco e, inoltre, consente anche di specificare la matrice di trasformazione grezza.

Da un punto di vista algoritmico, le funzioni translate() e rotate() sono delle funzioni di utilità che prendono in input i parametri, rispettivamente, in pixel e in gradi e creano una opportuna matrice di trasformazione da moltiplicare alle coordinate dei punti di quel blocco.

Fig. 1 Esempio di rotazione http://www.w3schools.com/cssref/trycss3_transform_inuse.htm

Matematicamente, le operazioni tra matrici sono una versione “condensata” delle operazioni tra sistemi di equazioni lineari. Nel nostro caso, abbiamo 2 equazioni per le due coordinate X e Y, che rappresentiamo in questo modo:

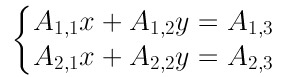
I termini A(1,1), A(1,2), ecc… sono i “coefficienti” del sistema, e possono essere rappresentati in forma compatta come la seguente matrice M di dimensioni 3x2:

In algebra, questo nuovo oggetto M può essere manipolato con delle operazioni di somma commutativa e moltiplicazione non commutativa (invertendo l’ordine degli operandi si ottengono due risultati diversi), ed il risultato di queste operazioni è nuovamente una matrice. Nel caso estremo, si può pensare al singolo numero reale come una matrice di dimensioni 1x1.

Non ci addentreremo nei dettagli della teoria, che richiederebbe un intero libro, ma basti pensare che usando questa notazione è possibile esprimere con formule molto semplici qualsiasi tipo di “applicazione lineare”, ossia tutte quelle funzioni che trasformano un oggetto da uno spazio all’altro. Nel nostro caso abbiamo a che fare con lo spazio dell’oggetto “prima” della trasformazione e quello “dopo” la trasformazione.

L’oggetto in sè rimane immutato da un punto di vista matematico, ma cambiano le sue coordinate nello spazio dell’osservatore, cioè la pagina HTML che l’utente visualizza sul browser. Ad esempio, la funzione rotate(alpha), dove “alpha” è un angolo espresso in gradi, verrà trasformato nella corrispondente matrice di rotazione:

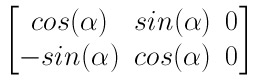
Questa matrice verrà poi “concatenata”, cioè moltiplicata a destra, alla matrice corrente di quel blocco. L’algoritmo di disegno userà poi questi coefficienti per risolvere il sistema di coordinate del blocco, e trovare quindi le coordinate corrette di ciascun pixel. Questo compito, computazionalmente molto oneroso, viene delegato da Internet Explorer 10 alla GPU che possiede centinaia di unità dedite al calcolo delle funzioni trigonometriche (seno, coseno, tangente e funzioni inverse) e unità vettoriali specializzate nella moltiplicazione e somma di matrici.

I calcoli necessari per le trasformazioni 2D, infatti, sono esattamente gli stessi che vengono impiegati anche nella grafica poligonale 3D, con l’unica differenza che aggiungendo la coordinata Z, le matrici avranno dimensione 4x3 (in realtà si aggiunge un’ulteriore riga per normalizzare lo spazio con la coordinata fittizia W, arrivando così a matrici 4x4). Quindi cambia solo il numero dei coefficienti (e di conseguenza il “peso” del calcolo), ma gli algoritmi e le formule matematiche sono gli stessi. Volendo calcolare a mano i coefficienti della matrice, è possibile specificarli in questo modo:

I valori 0.866 e 0.5 sono, rispettivamente, il coseno ed il seno dell’angolo di 30°, per cui l’oggetto subirà una rotazione intorno al proprio centro di questa quantità. E’ possibile sperimentare il metodo delle matrici usando questa pagina di esempio, e facendo sempre riferimento alla documentazione fornita a corredo di Internet Explorer 10 e del consorzio W3C.