|
|||||||
|
|
|
 |
|
|
Strumenti |
|
|
#21 | |
|
Bannato
Iscritto dal: Aug 2001
Città: Berghem Haven
Messaggi: 13526
|
Quote:
|
|
|
|

|
|
|
#22 | ||
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
Quote:
|
||
|
|

|
|
|
#23 | |
|
Bannato
Iscritto dal: Aug 2001
Città: Berghem Haven
Messaggi: 13526
|
Quote:
 |
|
|
|

|
|
|
#24 | |
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
|
|
|
|

|
|
|
#25 | |
|
Bannato
Iscritto dal: Aug 2001
Città: Berghem Haven
Messaggi: 13526
|
Quote:
Ultima modifica di lowenz : 23-08-2005 alle 18:41. |
|
|
|

|
|
|
#26 | |
|
Senior Member
Iscritto dal: Nov 2002
Città: Singularity
Messaggi: 894
|
Quote:
Però il problema di lowenz era notazionale... cioè perchè ci sono due notazioni per lo stesso numero, e come spiegarlo senza tirare in ballo i reali. Ma a quanto pare i decimali e i reali sono strettamente legati, e non è possibile evitare il passaggio R -> Q
__________________
echo 'main(k){float r,i,j,x,y=-15;while(puts(""),y++<16)for(x=-39;x++<40;putchar(" .:-;!/>"[k&7])) for(k=0,r=x/20,i=y/8;j=r*r-i*i+.1, i=2*r*i+.6,j*j+i*i<11&&k++<111;r=j);}'&>jul.c;gcc -o jul jul.c;./jul |Only Connect| "To understand is to perceive patterns" Isaiah Berlin "People often speak of their faith, but act according to their instincts." Nietzsche - Bayesian Empirimancer - wizardry |
|
|
|

|
|
|
#27 | |
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
|
|
|
|

|
|
|
#28 | |
|
Senior Member
Iscritto dal: Nov 2002
Città: Singularity
Messaggi: 894
|
Quote:
__________________
echo 'main(k){float r,i,j,x,y=-15;while(puts(""),y++<16)for(x=-39;x++<40;putchar(" .:-;!/>"[k&7])) for(k=0,r=x/20,i=y/8;j=r*r-i*i+.1, i=2*r*i+.6,j*j+i*i<11&&k++<111;r=j);}'&>jul.c;gcc -o jul jul.c;./jul |Only Connect| "To understand is to perceive patterns" Isaiah Berlin "People often speak of their faith, but act according to their instincts." Nietzsche - Bayesian Empirimancer - wizardry |
|
|
|

|
|
|
#29 | |
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
0.(3) sarebbe 0+3/10+3/100+..+ 3/10^k+.. MA se lo andiamo a moltiplicare non possiamo ripartire allo stesso modo... |
|
|
|

|
|
|
#30 | |
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
|
|
|
|

|
|
|
#31 | |
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
|
|
|
|

|
|
|
#32 |
|
Bannato
Iscritto dal: Jan 2005
Messaggi: 47
|
Ho abbastanza capito anche se alcune cose che avete detto non mi è stato facile capirle...
Grazie a tutti!!! |
|
|

|
|
|
#33 |
|
Member
Iscritto dal: Dec 2001
Città: Trieste
Messaggi: 41
|
[quote=lowenz]Ma la frazione è una divisione....che dà UN risultato: o 1 o 0.9.....
Buongiorno a tutti. Non e' corretto quello che affermi. L'ampliamento dell'insieme Z nell'insieme Q, tramite i metodi tipici dell'algebra relativi cioe' alla teoria degl'insiemi, e' stata fatta a causa dell'incompletezza di Z della divisione. Gli elementi di Q, (coppie ordinate di elementi di Z) , vengono ottenuti tramite una relazione di equivalenza. Ad esempio la coppia 1-2 e' equivalente alla coppia 2-4 . Soprattutto nell'insegnamento elementare, le classi di equivalenza cosi' formate, vengono chiamate frazioni. In seguito, nell'insegnamento elementare, si determina la rappresentazione decimale, tramite divisione della frazione, mostrando le rappresentazioni periodiche, ecc. che nel contesto puramente algebrico dell'insieme Q, non c'entrano nulla. La rappresentazione decimale di periodo 9, non puo' essere ottenuta da nessuna frazione A/B con A e B numeri relativi. Assomiglia al problema postato sotto di 1/0 = infinito. Una frazione con denominatore 0 non e' definita. Certamente alla retta reale R si potrebbero aggiungere i due punti +Inf e -Inf. Cio' sarebbe vantaggioso da un punto di vista topologico (legato cioe' alla struttura d'ordine) ma se applicassimo questi simboli alle usuali operazioni algebriche, perveremmo a delle contraddizioni. Questi due punti non esistono piu', una loro traccia e' la definizione d'intervallo o d'intorno. Scusate l'intromissione Ciao
__________________
Albert aveva ragione: Dio non gioca a dadi. By Walter ER Cassani |
|
|

|
|
|
#34 | ||
|
Bannato
Iscritto dal: Aug 2001
Città: Berghem Haven
Messaggi: 13526
|
Quote:
Infatti in Q, come tu dici, la rappresentazione decimale non conta nulla, peccato che sia fondamentale dal punto di vista pragmatico-intuitivo per noi Quote:
Ultima modifica di lowenz : 24-08-2005 alle 15:52. |
||
|
|

|
|
|
#35 | |
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
Il motivo per cui la rappresentazione 0.(9) non è corretta risiede nel come vengono costruiti i numeri decimali, di fatto il 9 periodico è escluso. Ma si potrebbe costruirli analogamente escludendo lo 0 periodico... non sarebbe molto pratico però! |
|
|
|

|
|
|
#36 | |
|
Member
Iscritto dal: Dec 2001
Città: Trieste
Messaggi: 41
|
Quote:
Per il primo punto possiamo vederla cosi' . Dal momento che le frazioni con denominatore 1 costituiscono in Q un insieme isomorfo a Z, possiamo supporre che ammettano due rappresentazioni decimali, X,0000000 e X-1,999999999 dove X è il numeratore, anche se nell'uso pratico si adopera la prima. Ciao
__________________
Albert aveva ragione: Dio non gioca a dadi. By Walter ER Cassani |
|
|
|

|
|
|
#37 | |
|
Bannato
Iscritto dal: Aug 2001
Città: Berghem Haven
Messaggi: 13526
|
Quote:
|
|
|
|

|
|
|
#38 | |
|
Senior Member
Iscritto dal: Mar 2001
Messaggi: 1910
|
Quote:
http://www.batmath.it/matematica/a_d...appr_reali.htm Consideriamo x Reale €[0,1[ Teorema 1: Esiste una ed una sola successione a1, a2, ..., an, ... di interi dell'intervallo [0,9] tali che, per ogni intero n≥1 si ha: 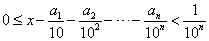 Teorema 2: La successione (ai) non può essere costantemente uguale a nove da un certo punto in poi. Definizione: Una successione a1, a2, ..., an, ...di interi dell'intervallo [0,9] si dice un allineamento decimale. Tale allineamento decimale si dice proprio se non è costantemente uguale a nove da un certo punto in poi. Indicheremo l'insieme di tutti gli allineamenti decimali con D, l'insieme di tutti gli allineamenti decimali propri con DP. Ora veniamo al subdolo tranello di Banus Teorema 3: La funzione 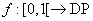 , che a x appartiene [0,1[ associa il suo allineamento decimale proprio, è una biiezione. , che a x appartiene [0,1[ associa il suo allineamento decimale proprio, è una biiezione.nelle rappresentazioni si usano gli allineamenti propri... |
|
|
|

|
|
|
#39 | |
|
Bannato
Iscritto dal: Aug 2001
Città: Berghem Haven
Messaggi: 13526
|
Quote:
|
|
|
|

|
|
|
#40 |
|
Member
Iscritto dal: Dec 2001
Città: Trieste
Messaggi: 41
|
Infatti la prima e' la rappresentazione propria e la seconda e' la rappresentazione impropria, che ha senso per chi ha voglia di farsi seghe mentali
Ciao Jumper
__________________
Albert aveva ragione: Dio non gioca a dadi. By Walter ER Cassani |
|
|

|

|
| Strumenti | |
|
|
Tutti gli orari sono GMT +1. Ora sono le: 13:30.






















