|
|||||||
|
|
|
 |
|
|
Strumenti |
|
|
#121 |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
quindi se ho la f(x) integrando ho la F(x) e derivando torno sulla f(x) ma..... è tutta qui la differenza tra f(x) ed F(x) ?
|
|
|

|
|
|
#122 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
f(x):= d/dx F(x) quindi si parte dal definire F(x) come ho scritto nei post precedenti. Poi si introduce la f(x) derivando la F(x).
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#123 |
|
Senior Member
Iscritto dal: Oct 2001
Messaggi: 1316
|
ciao a tutti, sono alle prese con alcuni problemi che, anche se banali, non riesco a risolvere. Devo riprendere in mano tutta la teoria perchè ho interrotto gli studi per alcuni anni e adesso ricominciare è difficile...comunque si tratta di questo problema:
2 scatole con tre pietre preziose in ciascuna, nella prima scatola 2 sono vere ed 1 falsa, nella seconda scatola 2 sono false ed una vera. a) scegliendo a caso 1 delle 2 scatole, qual è la probabilità di avere 2 pietre vere? b) si può estrarre 1 pietra senza conoscere però il contenuto delle scatole, qual è la strategia migliore per riuscire a prendere le 2 pietre vere? grazie e ciao.
__________________
MSI B450 Tomahawk | AMD Ryzen 5 3600 | 2x8GB Corsair Vengeance LPX DDR4 3000 | MSI GTX 1660 SUPER | HD SSD M2 500GB Samsung 970 EVO - 2x2TB SATA WD RED | Pioneer DVR-215 | Sharkoon AI7000 Silent | Corsair CX650M | EIZO CG2420 | Fritz!Box 7590 | Logitech Z-5500 | Tim Fibra |
|
|

|
|
|
#124 | |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
Quote:
sembra proprio il caso di una probabilità condizionata |
|
|
|

|
|
|
#125 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
a) la probabilità di scegliere la scatola con due pietre è 0.5 , dato che le scatole sono due. b)la prima volta peschi a caso, se trovi una pietra vera cambi scatola. Se trovi una pietra falsa peschi nella stessa scatola.ripeti questi pèassi finchè non trovi due pietre. si possono fare i conti per dimostrarlo formalmente ma ora ho sonno
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#126 |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
se ora voglio calcolare la probabilità nel continuo che la mia variabile aleatoria appartenga all'intervallo (alfa, beta) uso:
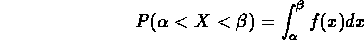 dove f(x) rappresenta una delle tante funzioni di distribuzione (normale, esponenziale etc...) per il caso del continuo, giusto ? e poi.... calcolato l'integrale quello che trovo e rappresentato graficamente è questo: 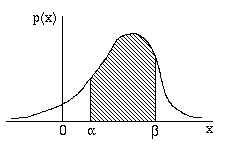 mentre la sua cumulata graficamente è quest'altra: 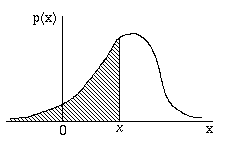
Ultima modifica di misterx : 11-12-2007 alle 10:07. |
|
|

|
|
|
#127 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#128 |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
quindi, scusa pietro, ultima chicca finale: nelle continue non si calcola banalmente la probabilità ma la densità di probabilità con l'integrale giusto ?
mi sa che.......forse....me lo hai gia detto 
Ultima modifica di misterx : 11-12-2007 alle 19:29. |
|
|

|
|
|
#129 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
integrando la funzione di densità di probabilità f(x) ottieni una probabilità nell'esempio che hai postato è scritto bene. vedi integrando la densità f(x) da alfa a beta ottieni la probabilità che x si trovi tra alfa e beta
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#130 |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
quindi tutti i numeri(punti) tra alfa e beta piccoli a piacere hanno pari probabilità ?
Ultima modifica di misterx : 11-12-2007 alle 20:16. |
|
|

|
|
|
#131 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
tu stai calcolando la probabilità che x assumi un valore tra alfa e beta. punto. e lo fai con l'integrale della densità di probabilità f(x)
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#132 | |
|
Senior Member
Iscritto dal: Feb 2004
Città: Marcon - VE (in trasferta a Ferrara)
Messaggi: 2312
|
Quote:
integrando f(x) in un intervallo qualsiasi si trova la probabilità che x sia compreso in quell'intervallo
__________________
Ed io non so chi va e chi resta. |
|
|
|

|
|
|
#133 |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
sono alle prese con la "funzione di ripartizione congiunta" e la definizione valida per il continuo ed il discreto è la seguente:
F(x,y)=(P(X<=x) intersezione P(Y<=y)) ma significa che la funzione di ripartizione lavora solo se le due variabili aleatorie hanno il medesimo valore, giusto ? Ma che diamine di significato ha una cosa del genere ? |
|
|

|
|
|
#134 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
X:numero di goal fatti da una squadra in una partita di calcio Y: voto preso da me all'esame F(2,25) è la probabilità che la squadra faccia due o meno goal e che io prenda all'esame un voto minore o uguale di 25.
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#135 | |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
Quote:

|
|
|
|

|
|
|
#136 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
non per forza devono essere variabili aleatorie correlate tra loro.
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#137 |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
|
|
|

|
|
|
#138 | |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
Quote:
 Quello che intendevo dire è che se il mio intervallo alfa beta lo penso come un alfa=140 e un beta=180 e penso alla probabilità di riuscire a pescarere una persona alta 175, significa che, mi va bene sia se è alta 140 o 180, quindi è come se tutti i punti tra 140 e 180 abbiano pari probabilità! Per me è solo una questzione di come la si pensa. Stesso valore ha se dico: studio che probabilità ho è che la mia variabile aleatoria assuma un valore compreso tra 140 e 180. |
|
|
|

|
|
|
#139 | |
|
Member
Iscritto dal: Nov 2005
Messaggi: 154
|
Quote:
__________________
"la scelta giusta non è sempre la più saggia,ma è quella che non porta con sè rimpianti" . pietro84 |
|
|
|

|
|
|
#140 |
|
Senior Member
Iscritto dal: Apr 2001
Città: Milano
Messaggi: 3736
|
boh, penso che sia solo una mia chiave di lettura.
Forse la più corretta è pensare che X assuma un valore compreso tra alfa beta e poi che tale probabilità che X assuma un valore tra quel range, la calcolo facendo l'integrale tra alfa e beta. |
|
|

|

|
| Strumenti | |
|
|
Tutti gli orari sono GMT +1. Ora sono le: 00:49.























