|
|||||||
|
|
|
 |
|
|
Strumenti |
|
|
#1 |
|
Senior Member
Iscritto dal: Dec 2009
Messaggi: 1056
|
[Generico]Ricorrenze
Ciao a tutti!
Allora sto imparando la complessità computazionale di alcuni algoritmi noti. Alcuni come quick sort oppure merge sort, usano la tecnica del divide et impera. Per calcolare la complessità di questi si usano le equzioni di ricorrenza... es merge sort nel caso peggiore è descritto da questa ricorrenza t(n) = c1 per n = 1 2T(n/2) + nc2 per n > 1 quindi t(n) = O(nlogn) Il prof ha spiegato nel corso soltanto il metodo iterativo...ora come dovrei procedere per dimostrare che t(n) = O(nlogn) ?  
|
|
|

|
|
|
#2 |
|
Senior Member
Iscritto dal: Jan 2006
Città: Perugia - San Benedetto del Tronto
Messaggi: 341
|
Uno dei metodi migliori per risolvere questo genere di equazioni di ricorrenza è l'uso di alberi di ricorsione:
http://www.dsi.unifi.it/~costa/lucid...Ricorsione.pdf Come ultima spiaggia c'è il Teorema dell'esperto, non sempre applicabile, che rappresenta una scorciatoia che è meglio evitare di prendere almeno quando si è all'inizio dello studio di equazioni di ricorrenza. Mi auguro soltanto che il fatto che tu non abbia accennato a questi metodi sia solo perchè il corso non è finito e il professore deve ancora spiegarteli  Cmq, dai un occhio alle slide. Se non ti torna chiedi pure. |
|
|

|
|
|
#3 |
|
Senior Member
Iscritto dal: Dec 2009
Messaggi: 1056
|
grazie per la risp
Il metodo dell'albero, correggimi se sbaglio, è la rappresentazione grafica del metodo iterativo? Cmq ho studiato un pò anche il metodo di sostituzione che procede per induzione matematica... Il teorema dell'esperto lo conosco superficialmente, ho letto delle cose sul libro però non ho voluto addentrarmi troppo in questa strada per via dei numerosi calcoli matematici che bisogna svolgere.  Non li ho mensionati perchè all'esame ho sentito dire che fanno svolgere le ricorrenze appunto con il metodo iterativo....che mi sembra anche il più facile...Ora è un pò tardi....domani vedrò meglio le slide che mi hai proposto.... |
|
|

|
|
|
#4 |
|
Senior Member
Iscritto dal: Dec 2009
Messaggi: 1056
|
uhm qui non ho capito
n^2 Sommatoria da i=0 a lg n 1/2^i < n^2 Somatoria i=0...infinito 1/2 ^i = 2 n^2 come si ricava 2 n^2 ?? poi per calcolare l'altezza dell'albero non ho capito i vari passaggi che fà: n --> 1/2n --> (1/2)^2 --> (1/2)^3 --> 1 perchè (1/2)^i n = 1 ??? |
|
|

|
|
|
#5 |
|
Senior Member
Iscritto dal: Dec 2009
Messaggi: 1056
|
 
|
|
|

|
|
|
#6 |
|
Senior Member
Iscritto dal: Jan 2006
Città: Perugia - San Benedetto del Tronto
Messaggi: 341
|
Le equazioni di ricorrenza sono sempre espresse dalla seguente formula generica:
Ovvero il mio problema si evolve in a sottoproblemi di dimensione n/b e per ciascun livello pago un dato costo f(n). L'equazione di ricorrenza del Mergesort è :  Quindi due sottoproblemi di dimensione n/2 e a ogni livello paghi un costo theta di n , ovvero un costo pari alla dimensione del problema stesso. Risolviamo con l'albero di ricorsione che, come hai detto te, altro non è che la visualizzazione sotto forma di albero del metodo iterativo (che sinceramente è molto scomodo e non si usa quasi mai). 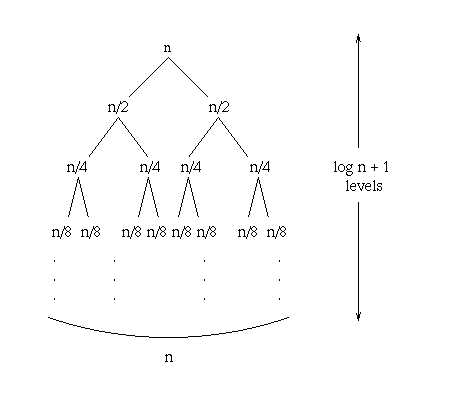 Quindi come vedi è molto facile costruire l'albero a partire dall'equazione. Metti semplicemente in ogni nodo la dimensione del problema a seconda del livello. Adesso: Quanto è alto l'albero? La prima cosa da fare per rispondere a questa domanda è capire con che "logica" si sviluppa la dimensione del tuo problema ed esprimerla in funzione dell'altezza. Livello 0 -> dimensione n livello 1-> dimensione n/2 livello 2 -> dimensione n/4 livello 3 -> dimensione n/8 e così via Che legame c'è tra il livello e la dimensione? Se ci fai caso, al livello i-esimo il tuo problema ha sempre dimensione Trovare l'altezza dell'albero significa capire a che profondità stanno le foglie. Le foglie sono all'interno dell'albero di ricorsione dei nodi il cui problema ha dimensione 1. Quindi se tu usi la regola generale che hai ricavato prima (in cui esprimevi la dimensione del problema in funzione del livello dell'albero), basta porre la formula che hai ricavato uguale ad 1 (perchè di fatto vuoi sapere quand'è che hai raggiunto la foglia). E risolvi l'equazione con i incognita. Se trovi quanto vale i per ottenere 1 trovi il livello delle foglie. Da cui, usando la definizione di logaritmo ( i infatti è il numero a cui devi elevare 2 per ottenere n) ottieni: Le foglie sono quindi al livello log(n) Ora puoi procedere con i calcoli per capire il costo dell'albero. La formula per trovare il costo dell'intero albero è: COSTO TOTALE = COSTO NODI INTERNI + COSTO FOGLIE
Ultima modifica di :.Blizzard.: : 03-02-2010 alle 16:33. |
|
|

|
|
|
#7 |
|
Senior Member
Iscritto dal: Dec 2009
Messaggi: 1056
|
grazie mille ora mi è molto più chiaro...
quando ricavo la sommatoria come faccio a ricavare O(nlogn)? poi un'altra cosa.... Quando ho questa ricorrenza Divido la struttura dati in due parti e applico la ricorsione su una sola delle due t(n) = t(n/2) + O(n) Non la posso sviluppare con un albero di ricorsione?? Grazie cmq Gentilissimo |
|
|

|
|
|
#8 |
|
Senior Member
Iscritto dal: Jan 2006
Città: Perugia - San Benedetto del Tronto
Messaggi: 341
|
E' una sommatoria indipendente dall'indice i. Se la leggi è come se ci fosse scritto "somma n per logn volte". Cioè logn*n. t(n) = t(n/2) + O(n) la sviluppi con l'albero di ricorsione esattamente come hai fatto per il merge. Però con l'unica differenza che invede di due nodi ne hai uno solo. Con questo esempio però i calcoli sono diversi, perchè non paghi più come nel merge theta di n per ogni livello (che ti usciva fuori sommando tutti i costi dei singoli nodi presenti sullo stesso livello). In questo esempio infatti, per quanto riguarda i costi hai: livello 0 --> costo n livello 1 --> costo n/2 livello 2 --> costo n/4 livello 3 --> costo n/8 Sempre il solito "trucchetto". Quanto paghi per ogni livello? Che regola generale hai? Ad ogni livello paghi Se rifai i conti come hai fatto prima per studiare la profondità e tutto il resto, vedrai che anche qui l'albero ha altezza Che è proprio la serie geometrica che ti ho scritto prima, con ragione |X| < 1 (in questo caso è 1/2).  e vale O(1) perchè hai comunque un numero, una costante dentro. Moltiplicato per n che hai portato fuori prima ottieni O(n). Matematicamente , durante i passaggi che ti ho riportato qui sopra, ho usato il maggiore uguale perchè utilizzi una maggiorazione per riportare la serie che hai a serie notevole. Ultima modifica di :.Blizzard.: : 03-02-2010 alle 18:19. |
|
|

|

|
| Strumenti | |
|
|
Tutti gli orari sono GMT +1. Ora sono le: 12:57.























