|
|||||||
|
|
|
 |
|
|
Strumenti |
|
|
#1 |
|
Senior Member
Iscritto dal: May 2004
Città: Londra (Torino)
Messaggi: 3692
|
[Vari] Contest 2: Ricerca
Sia data una matrice rettangolare mXn, preordinata per righe e per colonne.
Cio' significa che sia in ogni riga che in ogni colonna mi trovero' solo valori ascendenti. Guardate l'esempio 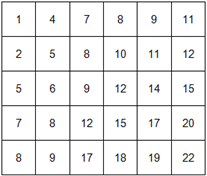 Quale e' la soluzione piu' efficiente per cercare se esiste almeno una volta un dato valore nella matrice? E se siamo in grado anche quale e' la complessita' della soluzione? Es: Esiste 13 nella matrice? ________________________________ Matrice di prova http://www.usaupload.net/d/y6jn9l2x9ap Formato: Comma spearated. Prima riga: DimX, DimY Righe Successive 15,17,19,22,27,....,1139,1150 etc. Da provarsi con i seguenti valori: [Non Presenti] 0 100 32538 20984 32767 [Presenti] 32539 26 11672 9790 14089
__________________
Se pensi che il tuo codice sia troppo complesso da capire senza commenti, e' segno che molto probabilmente il tuo codice e' semplicemente mal scritto. E se pensi di avere bisogno di un nuovo commento, significa che ti manca almeno un test. Ultima modifica di gugoXX : 19-07-2008 alle 23:27. |
|
|

|
|
|
#2 |
|
Senior Member
Iscritto dal: Jul 2005
Città: Bologna
Messaggi: 1130
|
Umh... magari dico una cazzata... ma una ricerca binaria su righe prima e colonne poi potrebbe andare?
Del tipo (prendendo l'esempio): parto dalla terza riga, terza colonna (9) 9 è minore di 13, quindi cerco (sempre ricerca binaria) nel sub-array verso destra. lo trovo? no... ricerca binaria sulla terza colonna, arrivo nella quarta riga, terza colonna (12) è ancora minore di 13, cerco come sopra verso destra (se fosse stato maggiore lo avrei cercato a sinistra) se esaurisco le righe non ho nessun risultato....
__________________
-> The Motherfucking Manifesto For Programming, Motherfuckers |
|
|

|
|
|
#3 |
|
Senior Member
Iscritto dal: May 2004
Città: Londra (Torino)
Messaggi: 3692
|
mmmh. Forse non ho capito bene.
Ma se il 13 fosse stato nella 2a riga, 7a colonna? L'avresti trovato?
__________________
Se pensi che il tuo codice sia troppo complesso da capire senza commenti, e' segno che molto probabilmente il tuo codice e' semplicemente mal scritto. E se pensi di avere bisogno di un nuovo commento, significa che ti manca almeno un test. |
|
|

|
|
|
#4 |
|
Member
Iscritto dal: Jul 2005
Messaggi: 291
|
forse dico una cavolata, se pensiamo la matrice come albero degenere ordinato la soluzione diventerebbe O(log(n)). nel senso che la root è il valore nel punto (0,0) che ha figli (1,0) e (0,1), (0,1) ha figli (0,2) e (1,1) mentre (1,0) ha figli (2,0) e (1,1). Così avremo che un nodo puo avere 2 padri (per questo l'albero è degenere) ma è crescente piu si scende, il che mi ricorda un Max-Heap il cui costo di ricerca è logaritmico sul numero dei nodi (si controlla la testa, se non è quella cercata si cancella e si crea una nuova testa come minimo dei figli e così via).
Al massimo per non fare l'albero degenere si sceglie un nodo a quale padre metterlo (casualmente). Almeno è quello che ho pensato in 30 secondi netti. Domani a mente fresca magari mi viene in mente qualcosa di meglio
__________________
CPU: Intel Core 2 Quad Q6600 - Mobo: Asus P5E - RAM:4x2GB DDR2 - sk video: Power Color ATI Radeon HD3870 - HD:Western Digital 750GB |
|
|

|
|
|
#5 |
|
Senior Member
Iscritto dal: Mar 2004
Messaggi: 1451
|
Partendo dall'elemento M,N e iterando sulla colonna n, e riga m, escludendo tutti i valori minori di x. Dopo di che riduco il mio intervallo di ricerca alla sottomatrice individuata, escludendo da questa le colonne nelle quali x non è incluso.
__________________
Ciao ~ZeRO sTrEsS~ |
|
|

|
|
|
#6 |
|
Senior Member
Iscritto dal: Jul 2002
Città: Reggio Calabria -> London
Messaggi: 12112
|
io dopo una quantità d'alcool che stenderebbe un elefante direi che bisogna innanzitutto partire dall'upper-left corner.
Poichè le righe e le colonne della mtrice sono crescenti in senso stretto, direi di proseguire lungo la diagonale principale della matrice fino a localizzare il numero precedente a quello cercato e il successivo (ovvero i due numeri che sulla diagonale siano rispettivamente minori e maggiori del numero cercato). al terzo passo arriviamo a 9 e quindi subito dopo c'è il 15. 9 è minore di 13 e 15 è maggiore. Perfetto. Abbiamo trovato la riga o la colonna che potenzialmente contengono il nostro numero x. A questo punto proseguirei, partendo dal numero 9 trovato lungo la diagonale, a destra seguendo la stessa riga dove si trova questo numero e in basso lungo la colonna che contiene il nostro numero 9. poichè incontriamo i numeri 12 in entrambi le direzioni seguiti da un numero maggiore del numero x possiamo escludere che il numero trovato sia in questa direzione. A questo punto, partendo dalla riga e dalla colonna i-esima - 1 e j-esima - 1 rispetto al numero 9 scandiamo le righe e le colonne a ritroso se e solo se il valore finale (i,N) (j,M) che esse presentano è minore di x. Ovviamente si prosegue fino a scandire a ritroso tutte le righe e le colonne che alla posizione (i,N) (j,M) presentano un valore > x. Non so se mi sono spiegato, ma così ad occhio dovrebbe andare...  ma non chiedetemi di calcolare la complessità computazionale che al massimo ve la calcolo domani prima di andare al mare  P.S. i e j rappresentano la riga e la colonna del numero minore di x appena trovato lungo la diagonale, ovvero 9.
__________________

Ultima modifica di ^TiGeRShArK^ : 19-07-2008 alle 03:03. |
|
|

|
|
|
#7 | |
|
Senior Member
Iscritto dal: Jul 2002
Città: Reggio Calabria -> London
Messaggi: 12112
|
Quote:
 P.S. su 4 visite che ha ricevuto il tuo allegato a quest'ora 3 le ho fatte io tentando di capirci qualcosa...mi sa che è un problema di tutti gli informatici essere scarsini coi disegni 
__________________

|
|
|
|

|
|
|
#8 |
|
Senior Member
Iscritto dal: Jul 2002
Città: Reggio Calabria -> London
Messaggi: 12112
|
Ora che ci penso, leggendo il post di shinya si aumenterebbe l'efficienza utilizzando una ricerca binaria tra l'indice finale della riga/colonna e andando a ritroso fino alla casella della diagonale che già sappiamo essere minore di x
__________________

|
|
|

|
|
|
#9 | |
|
Senior Member
Iscritto dal: May 2004
Città: Londra (Torino)
Messaggi: 3692
|
Quote:
Se la matrice avesse avuto una colonna in piu', e se ci fosse stato il 13 nella seconda riga, non l'avresti trovato.
__________________
Se pensi che il tuo codice sia troppo complesso da capire senza commenti, e' segno che molto probabilmente il tuo codice e' semplicemente mal scritto. E se pensi di avere bisogno di un nuovo commento, significa che ti manca almeno un test. |
|
|
|

|
|
|
#10 | |
|
Senior Member
Iscritto dal: Jul 2005
Città: Bologna
Messaggi: 1130
|
Quote:
Però il metodo proposto da tigershark non l'ho mica capito...  edit: leggendo il post di morskott mi viene in mente che la matrice cosi definita può essere vista come un heap (max-heap se la root è l'elemento [M,N]). Quindi 22 ha come figli 19 e 20. 19 ha come figli 18 e 17 e cosi via. Magari aiuta pensarla in questi termini... Cioè, si costruisce l'heap e si comincia a eliminare il nodo di valore massimo fino a che la root è maggiore di 13...umh...o forse no... edit2: ho buttato giù uno stralcio un pò tirato via in java basato su una priority queue (quella della libreria standard, che usa un heap al suo interno)... l'ho testato poco, ma sembra funzionicchiare... Codice:
import java.util.*;
public class Context2 {
public static void main(String[] args) {
List<Integer> m = Arrays.asList(1, 4, 7, 8, 9, 15, 2, 5, 8, 10, 11, 12, 5,
6, 9, 12, 14, 15, 7, 8, 12, 15, 17, 20, 8, 9, 17, 18, 19, 22);
PriorityQueue<Integer> p = new PriorityQueue<Integer>(11,
new Comparator<Integer>() {
public int compare(Integer o1, Integer o2) {
return -1 * o1.compareTo(o2);
}
});
for (int i : m)
p.add(i);
int guess = 13;
int elem;
do {
elem = p.poll();
if (elem == guess) {
System.out.println("Found!");
System.exit(0);
}
} while (elem > guess);
System.out.println("Not Found!");
}
}
__________________
-> The Motherfucking Manifesto For Programming, Motherfuckers Ultima modifica di shinya : 19-07-2008 alle 13:03. |
|
|
|

|
|
|
#11 | |
|
Senior Member
Iscritto dal: Jul 2002
Città: Reggio Calabria -> London
Messaggi: 12112
|
Quote:
 si applica una ricerca binaria sulla diagonale e si ricavano le posizioni del numero rispettivamente + piccolo e + grande di x (se x non è presente nella diagonale). Si memorizzano in due variabili, i e j, la riga e la colonna che contengono il numero immediatamente inferiore ad x sulla diagonale. a questo punto, poichè nei "bordi" inferiore e destro della matrice si trovano i numeri massimi di tutta la riga e di tutta la colonna si esamina il bordo inferiore della riga i-esima e il bordo destro della riga j-esima. Se il numero presente nelle due caselle appena analizzate è maggiore di x si inizia a scandire a ritroso la riga e la colonna, dal bordo verso il centro, sempre tramite ricerca binaria prendendo come estremi la riga m e la riga i e la casella n e la colonna j. e si continua così fino a che sui bordi non si incontra un numero minore di x. Mi sa che però faccio prima a scrivere uno pseudo-codice (con una ricerca semplice perchè non mi voglio complicare la vita a scrivere quella binaria) che si dovrebbe capire meglio il funzionamento..  Codice:
x = numero incognito
matrix[m, n] = matrice
int i = 0;
int j = 0;
while (matrix[i, j] <= x && i < m && j < n) {
i++;
j++;
}
if (matrix[i, j] == x) {
found();
}
a = i;
b = j;
while (matrix[m, j] > x && matrix[i, n] > x) {
for (int u = m; u > a; u--) {
if (matrix[u, j] == x)
found();
}
for (int v = n; v > b; v--) {
if (matrix[i, v] == x)
found();
}
i--;
j--;
}
notFound();
Per l'altra parte dell'algoritmo ora come ora mi sfugge la complessità...  Ad occhio si può calcolare, ma ancora ho il neurone troppo spento mi sa  P.S. spero che così si capisca.. 
__________________

Ultima modifica di ^TiGeRShArK^ : 19-07-2008 alle 13:19. |
|
|
|

|
|
|
#12 |
|
Senior Member
Iscritto dal: Dec 2005
Città: Istanbul
Messaggi: 1817
|
L'idea della ricerca binaria e' buona, pero' secondo me va portato "all'estremo".
Quando trovi la posizione del numero sulla diagonale ("n"), a quel punto puoi dividere la matrice in quattro sottomatrici. quella con righe e colonne strettamente inferiori ad 'n'. Quella con solo le righe strettamente inferiori, quella con solo le colonne strettamente inferiori, e la rimanente. Le due matrici che stanno sulla diagonale le possiamo escludere, in quanto siamo sicuri al 100% che contengono una tutti valori inferiori a quello cercato, l'altra tutti superiori. A questo punto ci rimangono due sottomatrici a cui possiamo applicare l'algoritmo ricorsivamente. Se mi dai qualche minuto posto anche del codice di esempio
__________________
One of the conclusions that we reached was that the "object" need not be a primitive notion in a programming language; one can build objects and their behaviour from little more than assignable value cells and good old lambda expressions. —Guy Steele |
|
|

|
|
|
#13 | |
|
Senior Member
Iscritto dal: Jul 2002
Città: Reggio Calabria -> London
Messaggi: 12112
|
Quote:

__________________

|
|
|
|

|
|
|
#14 |
|
Senior Member
Iscritto dal: Dec 2005
Città: Istanbul
Messaggi: 1817
|
Codice:
def positionOfGreatestLowerOrEqualThan( matrix, value, rowmin, colmin, rowmax,colmax ):
i = rowmin
j = colmin
while i < rowmax and j < colmax and matrix[i][j] <= value:
i+=1
j+=1
return [i,j]
def findNumber( matrix, value, rowmin, colmin, rowmax, colmax ):
if rowmin == rowmax or colmin == colmax:
return False
[i,j] = positionOfGreatestLowerOrEqualThan( matrix, value, rowmin, colmin, rowmax, colmax )
if matrix[i-1][j-1] == value:
return [i-1,j-1]
return findNumber( matrix, value, rowmin, j, i, colmax ) or findNumber( matrix, value, i, colmin, rowmax, j )
__________________
One of the conclusions that we reached was that the "object" need not be a primitive notion in a programming language; one can build objects and their behaviour from little more than assignable value cells and good old lambda expressions. —Guy Steele Ultima modifica di marco.r : 19-07-2008 alle 14:38. |
|
|

|
|
|
#15 |
|
Senior Member
Iscritto dal: Dec 2005
Città: Istanbul
Messaggi: 1817
|
Per inciso, per l'autore del thread: forse nel titolo intendevi dire "contest" ?
__________________
One of the conclusions that we reached was that the "object" need not be a primitive notion in a programming language; one can build objects and their behaviour from little more than assignable value cells and good old lambda expressions. —Guy Steele |
|
|

|
|
|
#16 | |
|
Senior Member
Iscritto dal: Dec 2005
Città: Istanbul
Messaggi: 1817
|
Quote:
 ) )
__________________
One of the conclusions that we reached was that the "object" need not be a primitive notion in a programming language; one can build objects and their behaviour from little more than assignable value cells and good old lambda expressions. —Guy Steele |
|
|
|

|
|
|
#17 |
|
Senior Member
Iscritto dal: May 2004
Città: Londra (Torino)
Messaggi: 3692
|
Non ho ancora letto le soluzioni, e mi paiono promettenti.
Forse c'e' ancora qualcosina da aggiustare. Provate ad applicare gli algoritmi anche a questo esempio  In cui ci sia da trovare il 10, il 12 oppure il 24
__________________
Se pensi che il tuo codice sia troppo complesso da capire senza commenti, e' segno che molto probabilmente il tuo codice e' semplicemente mal scritto. E se pensi di avere bisogno di un nuovo commento, significa che ti manca almeno un test. |
|
|

|
|
|
#18 |
|
Member
Iscritto dal: Jul 2005
Messaggi: 291
|
Una soluzione che almeno nel caso di test funziona è
Codice:
import java.util.*;
public class CercaNumero{
private static int h(int curr,int numero){
return numero-curr;
}
public static boolean isInConAStar(int[][] matrice,int numero){
class Coppia implements Comparable<Coppia>{
int i,j;
int goodness;
Coppia(int i,int j,int goodness){
this.i=i;
this.j=j;
this.goodness=goodness;
}
public int compareTo(Coppia c){
return this.goodness-c.goodness;
}
public boolean equals(Object o){
if (o!=null && this.getClass().equals(o.getClass())){
Coppia c=(Coppia)o;
return this.i==c.i && this.j==c.j;
}else
return false;
}
public int hashCode(){
return this.i+31*this.j;
}
}
SortedSet<Coppia> frontiera=new TreeSet<Coppia>();
frontiera.add(new Coppia(0,0,h(matrice[0][0],numero)));
while(!frontiera.isEmpty()){
Coppia current=frontiera.first();
if (matrice[current.i][current.j]==numero) return true;
System.out.println("Visistato il numero:"+String.valueOf(matrice[current.i][current.j]));
frontiera.remove(current);
int goodness_i=-1;
int goodness_j=-1;
try{
goodness_i=h(matrice[current.i+1][current.j],numero);
} catch(ArrayIndexOutOfBoundsException ex){};
try{
goodness_j=h(matrice[current.i][current.j+1],numero);
} catch(ArrayIndexOutOfBoundsException ex){};
if (goodness_i>=0){
if (goodness_j>=0){
frontiera.add(new Coppia(current.i,current.j+1,goodness_j));
frontiera.add(new Coppia(current.i+1,current.j,goodness_i));
}else{
frontiera.add(new Coppia(current.i+1,current.j,goodness_i));
}
}else{
if (goodness_j>=0){
frontiera.add(new Coppia(current.i,current.j+1,goodness_j));
}
}
}
return false;
}
public static void main(String[] args){
int[][] matrice=new int[3][3];
matrice[0][0]=1;
matrice[0][1]=4;
matrice[0][2]=7;
matrice[1][0]=2;
matrice[1][1]=5;
matrice[1][2]=8;
matrice[2][0]=5;
matrice[2][1]=6;
matrice[2][2]=9;
int numeroEsistente=8;
int numeroMinoreNonEsistente=3;
int numeroMaggioreNonEsistente=19;
boolean conNumeroEsistente=isInConAStar(matrice,numeroEsistente);
System.out.println("Finita prima ricerca");
boolean conNumeroNonEsistenteMinore=isInConAStar(matrice,numeroMinoreNonEsistente);
System.out.println("Finita seconda ricerca");
boolean conNumeroNonEsistenteMaggiore=isInConAStar(matrice,numeroMaggioreNonEsistente);
System.out.println("Finita terza ricerca");
System.out.println("A* - Con numero esistente:"+String.valueOf(conNumeroEsistente)+" - con numero non esistente minore:"+String.valueOf(conNumeroNonEsistenteMinore)+" - con numero non esistente maggiore:"+String.valueOf(conNumeroNonEsistenteMaggiore));
}
}
UPDATE: qualcuno me lo tradurrebbe in python che son curioso di vedere come esce?? Devo ancora calcolarci la complessità, che ad occhio sembra essere sublineare
__________________
CPU: Intel Core 2 Quad Q6600 - Mobo: Asus P5E - RAM:4x2GB DDR2 - sk video: Power Color ATI Radeon HD3870 - HD:Western Digital 750GB Ultima modifica di morskott : 19-07-2008 alle 16:41. |
|
|

|
|
|
#19 |
|
Senior Member
Iscritto dal: Mar 2004
Messaggi: 1451
|
puoi farmi un esempio della matrice con i valori?
__________________
Ciao ~ZeRO sTrEsS~ |
|
|

|
|
|
#20 | |
|
Senior Member
Iscritto dal: Jul 2002
Città: Reggio Calabria -> London
Messaggi: 12112
|
Quote:

__________________

|
|
|
|

|

|
| Strumenti | |
|
|
Tutti gli orari sono GMT +1. Ora sono le: 23:16.























