|
|||||||
|
|
|
 |
|
|
Strumenti |
|
|
#1 |
|
Junior Member
Iscritto dal: Oct 2005
Messaggi: 15
|
Funzione di dirichlet
Ciao,
sapete dirmi se qst funzione è ripetitiva e se esiste un modo x dimostrarlo? 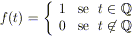
|
|
|

|
|
|
#2 | |
|
Senior Member
Iscritto dal: Nov 2002
Città: Singularity
Messaggi: 894
|
Quote:
Infatti se x è un numero razionale lo è anche x + q, dove q è razionale (Q è chiuso rispetto alla somma). Se x è irrazionale lo è anche y = x + q, perchè se non lo fosse avremmo x = y - q, quindi x razionale. Girando sulla rete ho letto che questa funzione ha un andamento che ricorda i frattali... ma non ho indagato ulteriormente
__________________
echo 'main(k){float r,i,j,x,y=-15;while(puts(""),y++<16)for(x=-39;x++<40;putchar(" .:-;!/>"[k&7])) for(k=0,r=x/20,i=y/8;j=r*r-i*i+.1, i=2*r*i+.6,j*j+i*i<11&&k++<111;r=j);}'&>jul.c;gcc -o jul jul.c;./jul |Only Connect| "To understand is to perceive patterns" Isaiah Berlin "People often speak of their faith, but act according to their instincts." Nietzsche - Bayesian Empirimancer - wizardry |
|
|
|

|
|
|
#3 |
|
Junior Member
Iscritto dal: Oct 2005
Messaggi: 15
|
è quello che penso anch'io, ma il prof dice che è impossibile determinare il periodo xche ci sono infiniti elementi che si susseguono senza un determinato ordine
sai dirmi dove cercare qlk dimostrazione? anche in inglese grazie |
|
|

|
|
|
#4 | |
|
Senior Member
Iscritto dal: Nov 2002
Città: Singularity
Messaggi: 894
|
Quote:
Comunque ho trovato il riferimento sul web: http://math.feld.cvut.cz/mt/txtb/4/txe3ba4s.htm La definizione di funzione periodica di periodo T è semplicemente: f(x) = f(x + T) per ogni x. Segue immediatamente che la funzione deve essere definita su tutto l'asse reale. Inoltre una funzione può avere più periodi. Se si parla di periodo al singolare in genere si considera quello minimo, ma non sempre è definito. Se la funzione ha due periodi T e T' commensurabili (mT' = nT) allora la funzione è anche periodica di periodo T/m (=T'/n), e puoi prendere questo come periodo. Ma se i due periodi non sono commensurabili, o nel caso della funzione di Dirichlet, avresti che il periodo è infinitesimo, non ha molto senso Per vedere l'andamento della funzione è utile scalare l'altezza in base al denominatore: http://mathworld.wolfram.com/DirichletFunction.html
__________________
echo 'main(k){float r,i,j,x,y=-15;while(puts(""),y++<16)for(x=-39;x++<40;putchar(" .:-;!/>"[k&7])) for(k=0,r=x/20,i=y/8;j=r*r-i*i+.1, i=2*r*i+.6,j*j+i*i<11&&k++<111;r=j);}'&>jul.c;gcc -o jul jul.c;./jul |Only Connect| "To understand is to perceive patterns" Isaiah Berlin "People often speak of their faith, but act according to their instincts." Nietzsche - Bayesian Empirimancer - wizardry |
|
|
|

|

|
| Strumenti | |
|
|
Tutti gli orari sono GMT +1. Ora sono le: 21:21.






















