Quote:
Originariamente inviato da thewebsurfer

rivedevo ancora la tua spiegazione: il denominatore di Cov(X,Y) al secondo passaggio, ossia σ_x*σ_y da dove viene?
Conosco la proprietÓ di linearitÓ della varianza, ma qui stiamo calcolando la Varianza di una somma, non Ŕ che posso aggiungere e togliere termini come voglio..quindi da dove viene?
|
Il punto Ŕ che la varianza Ŕ una forma omogenea di grado due, mentre la covarianza Ŕ una forma bilineare.
In generale, Ŕ vero che la varianza della somma non Ŕ la somma delle varianze. Il termine di correzione, per˛, Ŕ proprio il doppio della covarianza: e questo fa tornare i conti.
Ricapitolando:
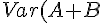=Var{A}+Var{B}+2Cov(A,B))
quindi,
=Var(X/%5Csigma_X)+Var(Y/%5Csigma_Y)+2Cov(X/%5Csigma_X,Y/%5Csigma_Y)) .
.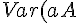={a^2}Var{A})
quindi,
=Var{X}/%5Csigma_X^2) e
e =Var{Y}/%5Csigma_Y^2) .
.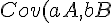=abCov(A,B))
quindi,
=Cov(X,Y)/(%5Csigma_X%5Csigma_Y)) .
.