Saro' un po' testa dura ma non capisco:
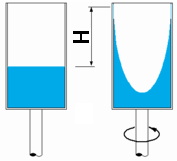
Problema nel ricavare matematicamente la funzione che descrive la superfice
di un liquido in rotazione.
m = massa
w = velocita' angolare in radianti al secondo
g = accellerazione di gravita' in metri al secondo^2
r = raggio in metri
E' data dall' equilibrio di 2 forze :
"centrifuga" = - m * w^2*r
e
gravitazionale = m * g
quindi la Derivata della funzione in un punto della curva e'
con
r = x
f'(x) = dy/dx = sen a / cos a = m * g/(- m * w^2*x)
semplifico la
m e ottengo
f'(x) = g/(- w^2*x) e mi fermo per
domandarvi.
A me risulta che
f'(x) = dy/dx = sen a / cos a ma, nei seguenti collegamenti
http://homepage.mac.com/astronomytea...tingmirror.pdf
http://www.nikhef.nl/~h73/kn1c/prakt...rim/1_4_02.pdf
e' considerata cosi' nel primo
f'(x) = dx/dy = w^2*x/g
sbagliata definizione di derivata
e corrispondenza tra i due lati dell'equazione
ma cosi' nell'altro
f'(x) = dy/dx = w^2*x/g corretta definizione di derivata ma
rovesciato il lato destro dell'equazione rispetto al lato sinistro
.
Si integra il secondo lato delle equazioni sopra per ricavare l'equazione primitiva cioe'
y = x^2 * w^2/(2*g) e visto che ruota a velocita' costante si puo'
scrivere
a=w^2/(2*g)=costante quindi
y = a*x^2 cioe'
l'equazione di una parabola che e' cio' che ci si dovrebbe aspettare; ma
non si capisce
perche' per farsela tornare questi scienziatoni, o rovesciano arbitrariamente
la definizione di derivata, o l'altro membro. 
Aiuto grazie