Quote:
|
Originariamente inviato da serbring
scusami avevo sbagliato a scrivere la funzione
|
OK, quindi il numeratore è una funzione olomorfa in tutto il piano complesso, mentre il denominatore si riscrive (z-4i)(z+4i).
Quindi il punto z=4i è un polo semplice, perché (z-4i)f(z) ammette limite in z=4i: per trovare il valore del residuo, basta calcolare il valore di tale limite, ossia, il valore di
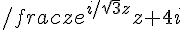
in z=4i. Tale valore è ovviamente
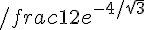
Nota: più in generale, se z0 è un polo di ordine n, allora vale la formula:
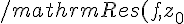=\frac{1}{(n-1)!}\lim_{z\to z_0}\frac{d^{n-1}}{dz^{n-1}}\left((z-z_0)^nf(z)\right))
come si vede subito considerando lo sviluppo in serie di Laurent di f in z0
