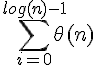
E' una sommatoria indipendente dall'indice
i. Se la leggi è come se ci fosse scritto "somma n per logn volte". Cioè logn*n.
t(n) = t(n/2) + O(n) la sviluppi con l'albero di ricorsione esattamente come hai fatto per il merge. Però con l'unica differenza che invede di due nodi ne hai uno solo. Con questo esempio però i calcoli sono diversi, perchè non paghi più come nel merge theta di n per ogni livello (che ti usciva fuori sommando tutti i costi dei singoli nodi presenti sullo stesso livello).
In questo esempio infatti, per quanto riguarda i costi hai:
livello 0 --> costo n
livello 1 --> costo n/2
livello 2 --> costo n/4
livello 3 --> costo n/8
Sempre il solito "trucchetto". Quanto paghi per ogni livello? Che regola generale hai?
Ad ogni livello paghi
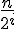
Se rifai i conti come hai fatto prima per studiare la profondità e tutto il resto, vedrai che anche qui l'albero ha altezza
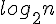
. E quando calcoli il costo dei nodi interni avrai:
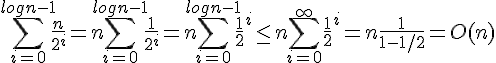
Che è proprio la serie geometrica che ti ho scritto prima, con ragione |X| < 1 (in questo caso è 1/2).

e vale O(1) perchè hai comunque un numero, una costante dentro. Moltiplicato per n che hai portato fuori prima ottieni O(n).
Matematicamente , durante i passaggi che ti ho riportato qui sopra, ho usato il maggiore uguale perchè utilizzi una
maggiorazione per riportare la serie che hai a serie notevole.