[gugoXX]

1) Sia data una lista di punti contenuti in uno spazio cubico, con coordinate tridimensionali in virgola mobile.
Il formato della lista e'

NP   Size
X1 Y1 Z1
X2 Y2 Z2
...
Xn Yn Zn

Dove NP e' il numero di punti (quindi le linee che seguono)
e Size e' un numero floating point pari alla dimensione del cubo di contenimento (quindi nessuna coordinata superera' tale valore)

Trovare ed enunciare la coppia di punti a distanza minima e la coppia di punti a distanza massima (e le distanze relative)

PS: Per quanto riguarda la formula della distanza tridimensionale in uno spazio euclideo, dati i punti
Pa di coordinate (Xa, Ya, Za) e Pb di coordinate (Xb, Yb, Zb)


(Da Wiki, sotto distanza Euclidea: )
E non ditemi che vi arenate sulla distanza 3D per favore. E' pieno di gente qui che vorrebbe fare giochi 3D, e chi si arena su una semplice distanza...

Lista dei punti: http://www.usaupload.net/d/cjepq9exi1j

2) Teorema: Sia dato un cubo di lato d ed un numero di particelle N
Esiste almeno una configurazione spaziale casuale delle N particelle tale per cui non esista nemmeno una coppia di particelle
con distanza c inferiore a
d / ³√N




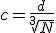
La semplice dimostrazione è lasciata come esercizio al lettore (Ho sempre sognato di scriverlo)

In pratica questo teorema ci assicura che tirando a caso molte volte la posizione di ciascuna delle N particelle, c'e' almeno una configurazione tale per cui le particelle non sono troppo vicine e distano tra loro almeno c.

Problema:
Si trovi almeno una configurazione spaziale (casuale) delle particelle nei seguenti casi:
d = 10 N = 5
d = 10 N = 10
d = 10 N = 50
d = 10 N = 100
d = 10 N = 200

PS: La soluzione di questo problema è in uso al CERN, per le condizioni iniziali di alcune simulazioni.

Domani posterò anche l'algoritmo di confronto a forza bruta.
Il primo esercizio serve come test di verifica per il secondo, non mi aspetto un'ottimizzazione particolare, anche se magari potrebbe essere interessante.