Eccomi!
Nell'approssimazione armonica, l'Hamiltoniano di un sistema allo stato solido si puo' scrivere come una somma di termini disaccoppiati (passando - dunque - ad un sistema di coordinate normali) e quindi l'energia sara' la somma delle energie di ogni singolo oscillatore:
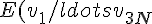=\sum_{\vec{k},s}(v_{\vec{k},s} + 1/2)\hbar\omega_s(\vec{k}))
dove gli indici v (sono 3N, se N é il numero di particelle) sono i numeri quantici di ogni oscillatore armonico, il vettore k è il vettore d'onda a cui è associata la frequenza omega (sono N e sono tutti contenuti nella prima zona di Brillouin, per periodicità) ed infine l'indice s corre sulle 3 componenti del vettore k.
La funzione di partizione del sistema sarà:
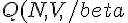=\sum_{v_1\ldots v_{3N}}\exp\left [ -\beta\sum_{\vec{k},s}(v_{\vec{k},s} + 1/2)\hbar\omega_s(\vec{k}) \right ] = \prod_{\vec{k},s}e^{\frac{-\beta\hbar\omega_s(\vec{k})}{2}}\left [\sum_v e^{[-\beta\hbar\omega_s(\vec{k})]^v}\right ]=\prod_{\vec{k},s}\frac{e^{\frac{-\beta\hbar\omega_s(\vec{k})}{2}}}{1-e^{-\beta\hbar\omega_s(\vec{k})} })
dove sono state sfruttate le proprietà dell'esponenziale (l'esponenziale della somme è il prodotto degli esponenziali) e il fatto che la somma sui numeri quantici è sempre la stessa per ogni numero.
L'energia per unità di volume sarà quindi:
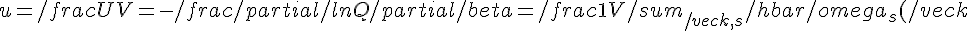 \left [ \frac{1}{2} + \frac{1}{e^{\beta\hbar\omega_s(\vec{k})}-1}\right ])
Il modello di Debye prevede di introdurre alcune approssimazioni che consentano di ottenere un'espressione analitica per la capacità termica, che si può scrivere in generale come
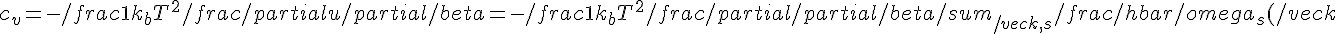}{e^{\beta\hbar\omega_s(\vec{k})}-1})
1) Si assume che omega sia lineare in k e che non dipenda dalla sua direzione:
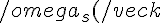 = c\cdot |\vec{k}| = ck)
2) Si assume che i vettori d'onda siano talmente fitti che da rendere lecita la sostituzione della sommatoria con un integrale esteso al volume della prima zona di Brillouin. In particolare, se il volume della prima zona è dato da
^3}{v}=N\frac{(2\pi)^3}{V})
dove v è il volume della cella elementare e V è il volume totale del solido, l'elemento di volume sarà dato dal rapporto fra il volume della cella e il numero di vettori:
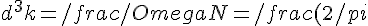^3}{V}\quad\Rightarrow\quad \frac{1}{V}\sum_{\vec{k}}\simeq \int_{\Omega}\frac{d^3k}{(2\pi)^3})
3) Poiché la prima zona di Brillouin è spesso complicata, si integra su una sfera che abbia il suo stesso volume, ovvero tale che
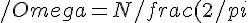^3}{V}=(2\pi)^3n=\frac{4}{3}\pi k_D^3\quad\Rightarrow\quad k_D^3=6\pi^2n)
con n densità numerale.
Andando a sostituire nell'espressione generale della calore specifico quanto stabilito si trova (dopo un macello di conti, purtroppo...):
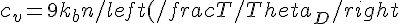^3\int_0^{\frac{\Theta_D}{T}} dx\frac{x^4e^x}{(e^x-1)^2})
con
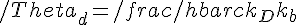
Ora a fare le cose per bene bisognerebbe ricostruire tutti i passaggi... magari se ne riparla

__________________
"Expedit esse deos, et, ut expedit, esse putemus" (Ovidio)
Il mio "TESSORO": SuperMicro 733TQ, SuperMicro X8DAI I5520, 2x Xeon Quad E5620 Westmere, 12x Kingston 4GB DDR3 1333MHz, 4x WD 1Tb 32MB 7.2krpm
