Quote:
|
Originariamente inviato da Matrixbob
Io avrei finito salvo qualche aggiustamento.
Solo 1 cosa qui non mi è molto chiara.
Come si fa a passare dalla forma integrale a quella differenziale? |
Esistono due importanti teoremi del calcolo differenziale che te lo permettono:
1) Per il teorema della divergenza:
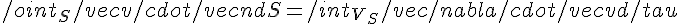
Ovvero il flusso di v attraverso una superficie chiusa S è uguale all'integrale di volume della divergenza di V dove il dominio di integrazione si intende il volume racchiuso dalla superficie chiusa S.
In questo modo, ad esempio:
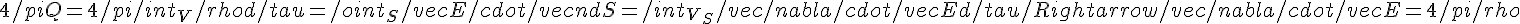
Dove il primo pezzo è il teorema di Gauss (prima legge di Maxwell in forma integrale) e il passaggio all'eguaglianza degli integrandi si può fare attraverso un processo di limite per cui si fa tendere la superficie a zero;
2) Per il teorema di Stokes o del rotore:
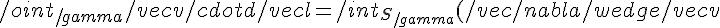\cdot \vec{n} dS)
Ovvero la circuitazione di v lungo la linea gamma è al flusso del rotore di v attraverso una superficie di bordo gamma
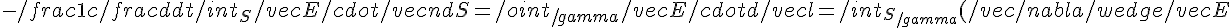 \cdot \vec{n} \Rightarrow \vec{\nabla} \wedge \vec{E} = -\frac{1}{c}\frac{\partial \vec{B}}{\partial t})
dove anche in questo caso l'uguaglianza degli integrandi va fatta con un processo di limite.
__________________
"Expedit esse deos, et, ut expedit, esse putemus" (Ovidio)
Il mio "TESSORO": SuperMicro 733TQ, SuperMicro X8DAI I5520, 2x Xeon Quad E5620 Westmere, 12x Kingston 4GB DDR3 1333MHz, 4x WD 1Tb 32MB 7.2krpm
